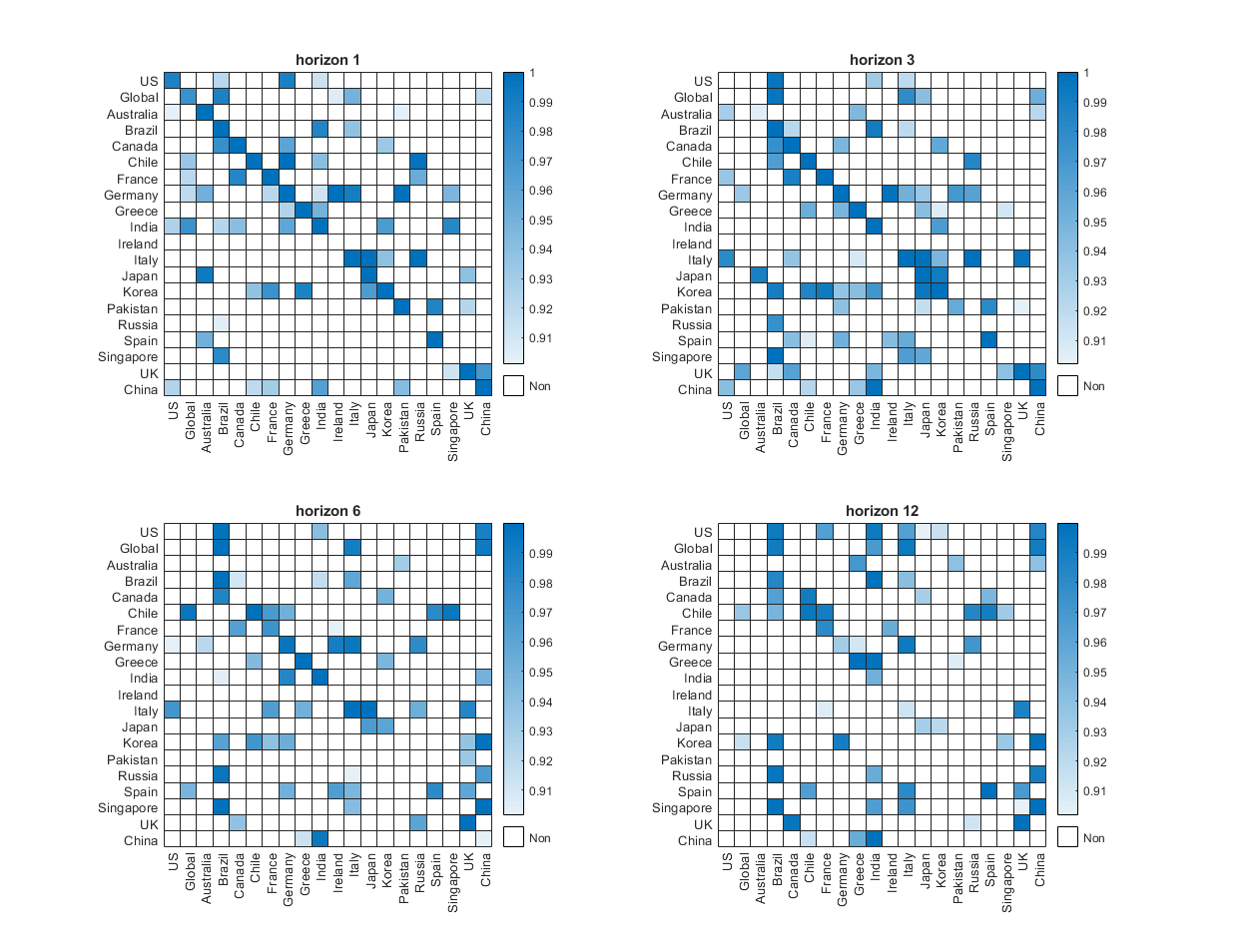
This paper presents a Wald test for multi-horizon Granger causality within a high dimensional sparse Vector Autoregression (VAR) framework. The null hypothesis focuses on the causal coefficients of interest in a local projection (LP) at a given horizon. Nevertheless, the post-double-selection method on LP may not be applicable in this context, as a sparse VAR model does not necessarily imply a sparse LP for horizon \(h > 1\). To validate the proposed test, we develop two types of de-biased estimators for the causal coefficients of interest, both relying on first-step machine learning estimators of the VAR slope parameters. The first estimator is derived from the Least Squares method, while the second is obtained through a two-stage approach that offers potential efficiency gains. We further derive heteroskedasticity- and autocorrelation-consistent (HAC) inference for each estimator. Additionally, we propose a robust inference method for the two-stage estimator, eliminating the need to correct for serial correlation in the projection residuals. Monte Carlo simulations show that the two-stage estimator with robust inference outperforms the Least Squares method in terms of the Wald test size, particularly for longer projection horizons. We apply our methodology to analyze the interconnectedness of policy-related economic uncertainty among a large set of countries in both the short and long run. Specifically, we construct a causal network to visualize how economic uncertainty spreads across countries over time. Our empirical findings reveal, among other insights, that in the short run (1 and 3 months), the U.S. influences China, while in the long run (9 and 12 months), China influences the U.S. Identifying these connections can help anticipate a country’s potential vulnerabilities and propose proactive solutions to mitigate the transmission of economic uncertainty.

This paper provides a user-friendly approach for moment-based estimation in high-dimensional contexts where many moments/instruments are available. Several economic applications involve many instruments. In this paper, we address the issue of efficient estimation in such frameworks. In fact, using many moment conditions can improve the efficiency of GMM-type estimators, as is well known, but can also lead to heavily biased estimates due to strong overidentification. We consider a specific setting where the large set of moments is derived from a single conditional moment restriction. The benchmark estimator we consider is the continuous updating GMM estimator (CUE) due to its relatively low bias under many moment conditions. We introduce a Ridge-type regularized version of CUE (RRCUE) to address the singularity problem of the weighting matrix under many moments. We show that the RRCUE estimator is consistent, asymptotically normal, and reaches the semi-parametric efficiency bound under an asymptotic regime where the regularization parameter goes to zero at a certain rate. We propose a data-driven approach for selecting the optimal regularization parameter based on cross-validation criteria. We evaluate the performance of the RRCUE through Monte Carlo simulations. Our results reveal that regularization reduces the dispersion problem of CUE and improves efficiency, although it introduces some bias that remains relatively low with a moderately large number of moments. In the specific linear instrumental variables framework, our estimator is shown to be competitive with some state-of-the-art estimators in the field. We apply our method to revisit the \cite{hall1999some} empirical application, which aims to estimate the effect of the quality of institutions and government policies, the so-called social infrastructure, on output per worker. Our empirical results are consistent with simulation results, providing estimates with better precision.